跳到主要内容

RepVGG - Making VGG-style ConvNets Great Again

· 阅读需 9 分钟
AsTheStarsFall

这篇笔记的写作者是AsTheStarsFall。

论文名称：RepVGG: Making VGG-style ConvNets Great Again

作者：Xiaohan Ding，Xiangyu Zhang，Ningning Ma，Jungong Han，Guiguang Ding，Jian Sun

Code：https://github.com/DingXiaoH/RepVGG

摘要​

  1. 提出了一种简单强大的CNN，推理时其拥有VGG类似的plain结构，仅由卷积和ReLU组成；训练时拥有多分支的拓扑结构
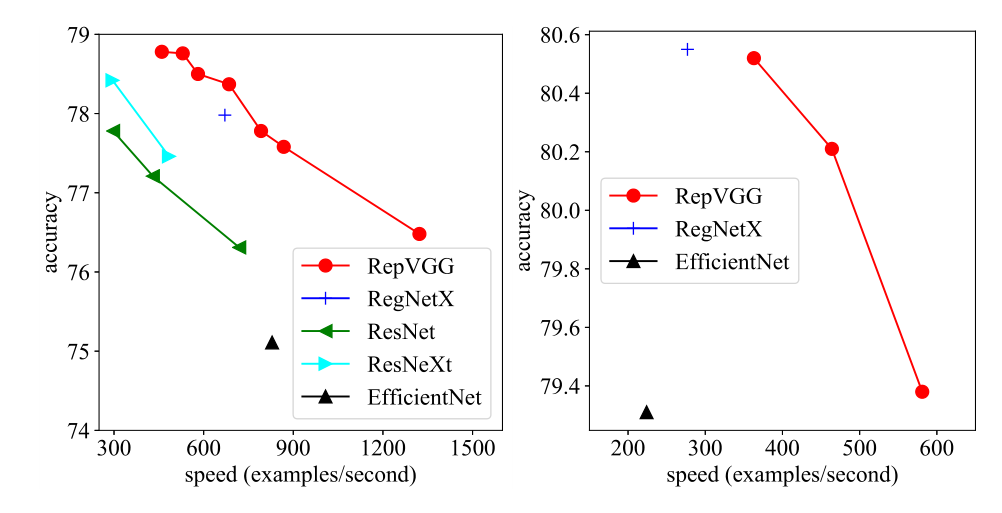
  2. 得益于结构重参化（re-parameterization）技术，RepVGG运行速度比ResNet-50快83%，比ResNet-101快101%，并且具有更高的精度。

介绍​

随着CNN在计算机视觉领域的成功，网络结构越来越复杂。这些复杂的结构相较于plain的网络结构虽然能够提供更高的精度，然是其缺点也是显而易见的：

  1. 复杂的多分支结构，各种各样的残差连接和concatenation增加了网络实现和修改难度，降低了推理速度和内存利用效率；
  2. 某些模块如深度卷积、channel shuffle等增加了内存访问的成本；

推理时间受到各种因素的影响，浮点运算（FLOPs）并不能准确反映实际速度，实际上VGG和NesNet在工业界还在大量使用着。而本文提出的RepVGG有以下优势：

  1. 与VGG相同的plain结构，没有任何分支；
  2. 只使用3×33\times 3卷积；
  3. 具体的架构没有使用自动搜索、手动优化、复合缩放等繁重的操作，仅仅使用了重参化。

相关工作​

From Single-path to Multi-branch​

主要是介绍各种网络结构的演变和进化，愈来愈多的复杂结构和结构搜索方法虽然一定程度上提高了模型性能，但是代价是巨大的计算资源。

Effective Training of Single-path Models​

已有一些工作尝试训练没有分支的网络，这些网络往往非常深，不能做到精确拟合，有工作提出了一种初始化方法用来训练10000层的plain卷积网络，但是这些网络既不方便也不实用。

Model Re-parameterization​

DiracNet将卷积层编码为W^=diag(a)I+diag(b)Wnorm\hat W=diag(a)I+diag(b)W_{norm}， W^\hat W表示最终使用的权重矩阵，a,ba,b是可学习的向量，WnormW_{norm}是可学习的归一化矩阵。与具有同等参数量的ResNet相比，精度有所下降。

实际上，DiracNet是将卷积核以另一种数学形式表达，使其更容易优化。

也有其他的工作使用不同的重参化方式，但是RepVGG的方法对于实现plain结构更为重要。

Winograd Convolution​

Winogard 是一种加速3×33\times 3卷积（stride=1）的经典算法，其乘法量减少到原来的4/9，因此RepVGG重参化之后仅仅使用3×33\times3卷积来加速推理。

image-20210915133349387

Building RepVGG via Structural Re-param​

选择plain网络结构的原因

Simple is Fast, Memory-economical, Flexible​

使用简单的卷积神经网络（比如VGG）是因为其拥有至少以下三个优点：

  1. 快速

    很多网络拥有用比VGG更小的理论浮点计算量（FLOPs），但是其实际推理速度并没有VGG快速，FlOPs不能代表网络的计算速度。

    计算速度主要与两个重要因素有关：

    • 内存访问成本（MAC）：虽然残差连接和concatenation几乎可以忽略不计，但是其提高了内存访问成本（残差连接需要提高一倍的内存占用），此外，组卷积也会提高时间；
    • 并行度：并行度是另一个重要因素，Inseption和一些自动搜索架构使用了很多小操作（small operators），这大大降低了网络的并行度。

  2. 内存经济

    对于多分支的网络拓扑结构，每个分支的输出都必须保留，直到addition或concatenation操作完成，这会大大提高内存占用，如下图：

    image-20210915135344621

    而plain的网络结构能够及时释放内存，并且设计专门的硬件时可以将更多的计算单元集成到芯片上。

  3. 灵活

多分支的网络结构限制了本身的灵活性，很难进行修改，牵一发而动全身，并且剪枝技术也受到很多限制。相比之下，plain结构允许我们根据需求自由配置歌层，并进行修剪以获得更好的性能效率权衡。

Training-time Multi-branch Architecture​

plain的网络结构有一个致命的缺点——性能差，使用BN层的情况下，VGG-16仅仅能达到72% top-1准确率；

受到ResNet的启发，使用一个y=x+f(x)y=x+f(x)，当x、f(x)x、f(x)不匹配时，使用1×11\times 1的卷积层，则y=g(x)+f(x)y=g(x)+f(x)；

ResNet成功的一个解释是，这种多分支的结构使得网络成为各个浅层模型的隐式集成，具体来说，有n个Block时，模型可以被解释为2n2^n个模型的集合，因为每个块将流分成两条路径。

虽然多分支结构在推理方面存在缺陷，但是其十分有利于训练；于是构建了一个y=x+g(x)+f(x)y=x+g(x)+f(x)的结构，堆叠了n层，从上述可知，这意味着3n3^n个模型的集合。

Re-param for Plain Inference-time Model​

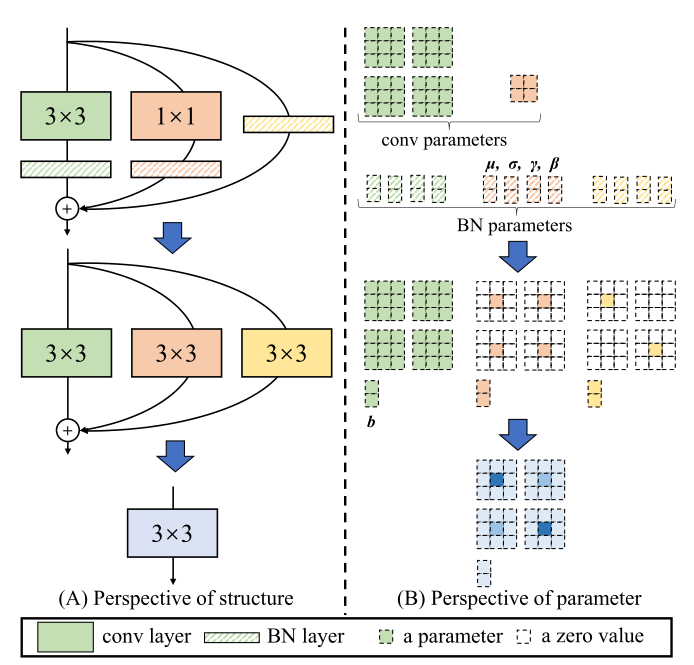
image-20210915185030692

推理之前会进行重参数化，RepVGG的模块结构如上图所示，由3×3,1×1,identity3\times 3,1\times 1,identity组成，将这些全部变为3×33\times3卷积相加即可实现ReP。

1×11\times1：赋值给3×33\times3矩阵的中心，其余为0即可，具体实现可以使用zero-padding

identity：将3×33\times3矩阵中心赋值为1，其余为0

padding的代码为

    def _pad_1x1_to_3x3_tensor(self, kernel1x1):
        if kernel1x1 is None:
            return 0
        else:
            return torch.nn.functional.pad(kernel1x1, [1, 1, 1, 1])

BN：

设卷积Conv(x)=W(x)+bConv(x)=W(x)+b，BN为BN(x)=γ(x−mean)var+βBN(x)=\gamma\frac{(x-mean)}{\sqrt{var}}+\beta

带入可得:

BN(Conv(x))=γ(W(x)+b−mean)var+β=γ∗W(x)var+(γ∗(b−mean)var+β)\begin{align} BN(Conv(x))&=\gamma\frac{(W(x)+b-mean)}{\sqrt{var}}+\beta\\&=\frac{\gamma*W(x)}{\sqrt{var}}+(\frac{\gamma*(b-mean)}{\sqrt{var}}+\beta) \end{align}

注意后面为卷积的偏置项

    def _fuse_bn_tensor(self, branch):
        if branch is None:
            return 0, 0
        if isinstance(branch, nn.Sequential):
            kernel = branch.conv.weight
            running_mean = branch.bn.running_mean
            running_var = branch.bn.running_var
            gamma = branch.bn.weight
            beta = branch.bn.bias
            eps = branch.bn.eps
        else:
            assert isinstance(branch, nn.BatchNorm2d)
            if not hasattr(self, 'id_tensor'):
                input_dim = self.in_channels // self.groups
                kernel_value = np.zeros(
                    (self.in_channels, input_dim, 3, 3), dtype=np.float32)
                for i in range(self.in_channels):
                    kernel_value[i, i % input_dim, 1, 1] = 1
                self.id_tensor = torch.from_numpy(
                    kernel_value).to(branch.weight.device)
            kernel = self.id_tensor
            running_mean = branch.running_mean
            running_var = branch.running_var
            gamma = branch.weight
            beta = branch.bias
            eps = branch.eps
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta - running_mean * gamma / std

这里BN的running_mean和running_var是从开始训练就一直记录的，并且其计算场景是online的，因为事先不知道会有多少数据，所以只能每次增量计算。计算公式为：

meant=∑i=1txiNt=meant−1⋅(Nt−1+xt)Nt=meant−1+1Nt(xi−meant−1)mean_{t}=\frac{\sum_{i=1}^{t}x_i}{N_t}=\frac{mean_{t-1}\cdot(N_{t-1}+x_t)}{N_t}=mean_{t-1}+\frac{1}{N_t}(x_i-mean_{t-1})

代码如下

class RunningStats:

    def __init__(self):
        self.n = 0
        self.old_m = 0
        self.new_m = 0
        self.old_s = 0
        self.new_s = 0
    
    def clear(self):
        self.n = 0
        
    def push(self, x):
        self.n += 1
        
        if self.n == 1:
            self.old_m = self.new_m = x
            self.old_s = 0
        else:
            self.new_m = self.old_m + (x - self.old_m) / self.n # 更新
            self.new_s = self.old_s + (x - self.old_m) * (x - self.new_m)
            
            self.old_m = self.new_m
            self.old_s = self.new_s

    def mean(self):
        return self.new_m if self.n else 0.0
    
    def variance(self):
        return self.new_s / (self.n - 1) if self.n > 1 else 0.0

Architectural Specification​

image-20210915210000222

上图表示RepVGG各个阶段的输出，第一个阶段使用Stride=2的conv来进行下采样

第一阶段输入分辨率高，仅使用一个卷积层，在最后一个阶段（14×1414\times14）使用更多的卷积层

使用Efficient neural networks中经典的multiplier来控制网络大小和性能的平衡，具体看论文