Mukund Sundararajan , Ankur Taly , Qiqi Yan
We study the problem of attributing the prediction of a deep network to its input features, a problem previously studied by several other works. We identify two fundamental axioms---Sensitivity and Implementation Invariance that attribution methods ought to satisfy. We show that they are not satisfied by most known attribution methods, which we consider to be a fundamental weakness of those methods. We use the axioms to guide the design of a new attribution method called Integrated Gradients. Our method requires no modification to the original network and is extremely simple to implement; it just needs a few calls to the standard gradient operator. We apply this method to a couple of image models, a couple of text models and a chemistry model, demonstrating its ability to debug networks, to extract rules from a network, and to enable users to engage with models better.
本文介绍了一种神经网络的可视化方法:积分梯度(Integrated Gradients),是一篇 2016-2017 年间的工作。
所谓可视化,简单来说就是对于给定的输入 x x x F ( x ) F(x) F ( x ) x x x x x x 归因(Attribution)。一个朴素的思路是直接使用梯度 ∇ x F ( x ) \nabla _{x}F(x) ∇ x F ( x ) x x x
朴素梯度 考虑一个图片分类系统,将输入图 x x x C C C c ∈ C c\in C c ∈ C S c ( x ) S_c(x) S c ( x ) x x x
c l a s s ( x ) = arg max c ∈ C S c ( x ) class(x)=\argmax_{c\in C} S_c(x) c l a ss ( x ) = c ∈ C arg max S c ( x ) 如果S c ( x ) S_c(x) S c ( x ) S c ( x ) S_c(x) S c ( x )
M c ( x ) = ∇ x S c ( x ) M_c(x)=\nabla_x S_c(x) M c ( x ) = ∇ x S c ( x ) 这里的M c ( x ) M_c(x) M c ( x ) x x x c c c
这种方法在实际操作中确实能显示出与分类结果相关的区域,但求得的 saliency maps 通常在视觉上有很多的噪点(对这些噪点作用目前还不清楚,有可能这些噪点看似随机,实际上对网络的运作有很大的影响,也有可能这些噪点本身就不重要),但正是因为这些噪点的存在,导致只能大致确定相关区域的位置,而不能给出符合人类理解的结果,如下图:
产生噪点的可能原因在于S c S_c S c R e L U ReLU R e LU S x S_x S x
下面给一特定图片加一微小的扰动,观察其中一个像素的偏导数的变化情况:
从数学层面推导,它就是基于泰勒展开
F ( x + Δ x ) − F ( x ) ≈ ⟨ ∇ x F ( x ) , Δ x ⟩ = ∑ i [ ∇ x F ( x ) ] i Δ x i \begin{align} F(x+\Delta x)-F(x)&\approx \left \langle \nabla_xF(x),\Delta x \right \rangle =\sum_i[\nabla_xF(x)]_i\Delta x_i \end{align} F ( x + Δ x ) − F ( x ) ≈ ⟨ ∇ x F ( x ) , Δ x ⟩ = i ∑ [ ∇ x F ( x ) ] i Δ x i 其中Δ x i \Delta x_i Δ x i Δ x i = ϵ i \Delta x_i=\epsilon_i Δ x i = ϵ i ϵ i \epsilon_i ϵ i
∇ x F ( x ) \nabla_xF(x) ∇ x F ( x ) x x x [ ∇ x F ( x ) ] i [\nabla_xF(x)]_i [ ∇ x F ( x ) ] i i i i Δ x i \Delta x_i Δ x i [ ∇ x F ( x ) ] i [\nabla_xF(x)]_i [ ∇ x F ( x ) ] i F ( x + Δ x i ) F(x+\Delta x_i) F ( x + Δ x i ) F ( x ) F(x) F ( x )
[ ∇ x F ( x ) ] i [\nabla_xF(x)]_i [ ∇ x F ( x ) ] i i i i ∣ [ ∇ x F ( x ) ] i ∣ |[\nabla_xF(x)]_i| ∣ [ ∇ x F ( x ) ] i ∣ i i i
这种思路比较简单,很多时候它确实可以成功解释一些模型,但是它也有明显的缺点。一旦进入到了饱和区(典型的就是 ReLU 的负半轴),梯度就为 0 了,那就揭示不出什么有效信息了。
按照论文中的描述就是说违反了S e n s i t i v i t y Sensitivity S e n s i t i v i t y
公理: S e n s i t i v i t y Sensitivity S e n s i t i v i t y
定义:如果对于所有仅在一个特征上具有不同取值的输入 (i n p u t input in p u t ( b a s e l i n e ) (baseline) ( ba se l in e ) S e n s i t i v i t y Sensitivity S e n s i t i v i t y
举个例子,一个单变量R e L U ReLU R e LU
f ( x ) = 1 − R e L U ( 1 − x ) = { x , x < 1 1 , x ≥ 1 f(x)=1-ReLU(1-x)=\left\{\begin{matrix} x,x<1\\ 1,x\geq 1 \end{matrix}\right. f ( x ) = 1 − R e LU ( 1 − x ) = { x , x < 1 1 , x ≥ 1 假设基线( b a s e l i n e ) (baseline) ( ba se l in e ) x = 0 x=0 x = 0 x = 2 x=2 x = 2 f ( 0 ) = 0 , f ( 2 ) = 1 f(0)=0,f(2)=1 f ( 0 ) = 0 , f ( 2 ) = 1 S e n s i t i v i t y Sensitivity S e n s i t i v i t y
首先,输入x = 2 x=2 x = 2 x = 0 x=0 x = 0 f ( x = 2 ) = 1 f(x=2)=1 f ( x = 2 ) = 1 f ( x = 0 ) = 0 f(x=0)=0 f ( x = 0 ) = 0 S e n s i t i v i t y Sensitivity S e n s i t i v i t y x x x x = 2 x=2 x = 2 S e n s i t i v i t y Sensitivity S e n s i t i v i t y
积分梯度 参照背景 首先,我们需要换个角度来理解原始问题:我们的目的是找出比较重要的分量,但是这个重要性不应该是绝对的,而应该是相对的。比如,我们要找出近来比较热门的流行词,我们就不能单根据词频来找,不然找出来肯定是“的”、“了”之类的停用词,我们应当准备一个平衡语料统计出来的“参照”词频表,然后对比词频差异而不是绝对值。这就告诉我们,为了衡量 x x x x ˉ \bar{x} x ˉ
很多场景下可以简单地让x ˉ = 0 \bar{x}=0 x ˉ = 0 x ˉ \bar{x} x ˉ F ( x ˉ ) F(\bar{x}) F ( x ˉ ) x ˉ \bar{x} x ˉ F ( x ˉ ) − F ( x ) F(\bar{x})−F(x) F ( x ˉ ) − F ( x ) x x x x ˉ \bar{x} x ˉ
如果还是用近似展开,那么我们可以得到
F ( x ˉ ) − F ( x ) ≈ ∑ i [ ∇ x F ( x ) ] i [ x ˉ − x ] i \begin{align} F(\bar{x})-F(x)\approx\sum_i[\nabla_x F(x)]_i[\bar{x}-x]_i \end{align} F ( x ˉ ) − F ( x ) ≈ i ∑ [ ∇ x F ( x ) ] i [ x ˉ − x ] i 对于上式,我们就可以有一种新的理解
从 x x x x ˉ \bar{x} x ˉ F ( x ˉ ) − F ( x ) F(\bar{x})-F(x) F ( x ˉ ) − F ( x ) [ ∇ x F ( x ) ] i [ x ˉ − x ] [\nabla_x F(x)]_i[\bar{x}-x] [ ∇ x F ( x ) ] i [ x ˉ − x ] ∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ |[\nabla_xF(x)]_i[\bar{x}-x]_i| ∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ i i i
当然,不管是[ ∇ x F ( x ) ] i [\nabla_xF(x)]_i [ ∇ x F ( x ) ] i ∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ |[\nabla_xF(x)]_i[\bar{x}-x]_i| ∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣
积分恒等 前面∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ |[\nabla_xF(x)]_i[\bar{x}-x]_i| ∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ ( 2 ) (2) ( 2 )
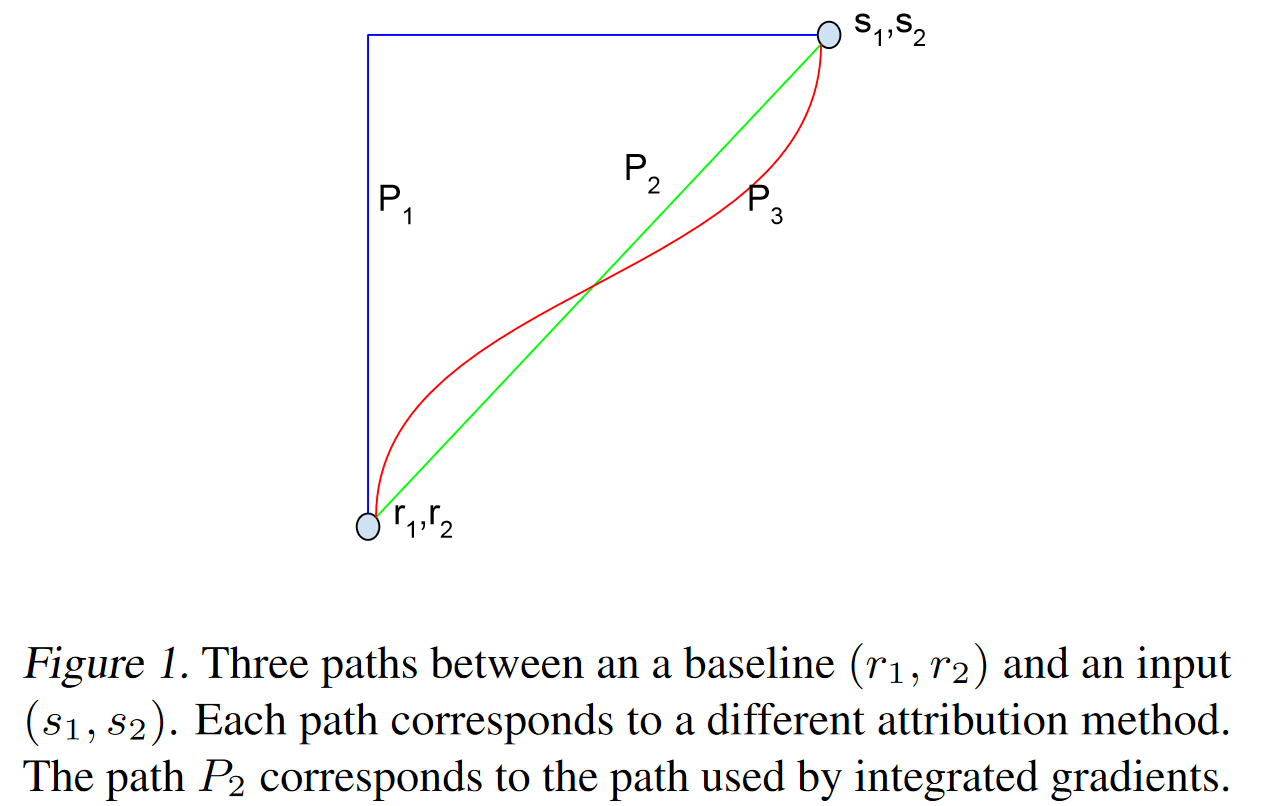
设γ ( a ) , a ∈ [ 0 , 1 ] \gamma(a),a\in[0,1] γ ( a ) , a ∈ [ 0 , 1 ] x x x x ˉ \bar{x} x ˉ γ ( 0 ) = x , γ ( 1 ) = x ˉ \gamma(0)=x,\gamma(1)=\bar{x} γ ( 0 ) = x , γ ( 1 ) = x ˉ
F ( x ˉ ) − F ( x ) = F ( γ ( 1 ) ) − F ( γ ( 0 ) ) = ∫ 0 1 d F ( γ ( α ) ) d α d α = ∫ 0 1 ⟨ ∇ γ F ( γ ( α ) ) , γ ′ ( α ) ⟩ d α = ∑ i ∫ 0 1 [ ∇ γ F ( γ ( α ) ) ] i [ γ ′ ( α ) ] i d α \begin{aligned} F(\bar{x})-F(x) &=F(\gamma(1))-F(\gamma(0)) \\ &=\int_{0}^{1} \frac{d F(\gamma(\alpha))}{d \alpha} d \alpha \\ &=\int_{0}^{1}\left\langle\nabla_{\gamma} F(\gamma(\alpha)), \gamma^{\prime}(\alpha)\right\rangle d \alpha \\ &=\sum_{i} \int_{0}^{1}\left[\nabla_{\gamma} F(\gamma(\alpha))\right]_{i}\left[\gamma^{\prime}(\alpha)\right]_{i} d \alpha \end{aligned} F ( x ˉ ) − F ( x ) = F ( γ ( 1 )) − F ( γ ( 0 )) = ∫ 0 1 d α d F ( γ ( α )) d α = ∫ 0 1 ⟨ ∇ γ F ( γ ( α )) , γ ′ ( α ) ⟩ d α = i ∑ ∫ 0 1 [ ∇ γ F ( γ ( α )) ] i [ γ ′ ( α ) ] i d α 可以看到,式子(3)具有跟式(2)相同的形式,只不过将[ ∇ x F ( x ) ] i [ x ˉ − x ] i [\nabla_xF(x)]_i[\bar{x}-x]_i [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∫ 0 1 [ ∇ γ F ( γ ( α ) ) ] i [ γ ′ ( α ) ] i d α \int_{0}^{1}\left[\nabla_{\gamma} F(\gamma(\alpha))\right]_{i}\left[\gamma^{\prime}(\alpha)\right]_{i} d \alpha ∫ 0 1 [ ∇ γ F ( γ ( α )) ] i [ γ ′ ( α ) ] i d α
∣ ∫ 0 1 [ ∇ γ F ( γ ( α ) ) ] i [ γ ′ ( α ) ] i d α ∣ \begin{align} \left|\int_{0}^{1}\left[\nabla_{\gamma} F(\gamma(\alpha))\right]_{i}\left[\gamma^{\prime}(\alpha)\right]_{i} d \alpha\right| \end{align} ∣ ∣ ∫ 0 1 [ ∇ γ F ( γ ( α )) ] i [ γ ′ ( α ) ] i d α ∣ ∣ 作为第i i i
作为最简单的方案,就是将γ ( a ) \gamma(a) γ ( a )
γ ( a ) = ( 1 − a ) x + a x ˉ \gamma(a)=(1-a)x+a\bar{x} γ ( a ) = ( 1 − a ) x + a x ˉ 这时候积分梯度具体化为
∣ [ ∫ 0 1 ∇ γ F ( γ ( α ) ) ∣ γ ( α ) = ( 1 − α ) x + α x ˉ d α ] i [ x ˉ − x ] i ∣ \left|\left[\left.\int_{0}^{1} \nabla_{\gamma} F(\gamma(\alpha))\right|_{\gamma(\alpha)=(1-\alpha) x+\alpha \bar{x}} d \alpha\right]_{i}[\bar{x}-x]_{i}\right| ∣ ∣ [ ∫ 0 1 ∇ γ F ( γ ( α )) ∣ ∣ γ ( α ) = ( 1 − α ) x + α x ˉ d α ] i [ x ˉ − x ] i ∣ ∣ 所以相比于∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ |[\nabla_xF(x)]_i[\bar{x}-x]_i| ∣ [ ∇ x F ( x ) ] i [ x ˉ − x ] i ∣ ∫ 0 1 [ ∇ γ F ( γ ( α ) ) ] i [ γ ′ ( α ) ] i d α \int_{0}^{1}\left[\nabla_{\gamma} F(\gamma(\alpha))\right]_{i}\left[\gamma^{\prime}(\alpha)\right]_{i} d \alpha ∫ 0 1 [ ∇ γ F ( γ ( α )) ] i [ γ ′ ( α ) ] i d α ∇ x F ( x ) \nabla_xF(x) ∇ x F ( x ) x x x x ˉ \bar{x} x ˉ
离散近似 最后这个积分着实有点恐怖。积分梯度可以通过求和来高效地做近似计算,只需要将基线x ˉ \bar{x} x ˉ x x x
∣ [ 1 n ∑ k = 1 n ( ∇ γ F ( γ ( α ) ) ∣ γ ( α ) = ( 1 − α ) x + α x ˉ , α = k / n ) ] i [ x ˉ − x ] i ∣ \left|\left[\frac{1}{n} \sum_{k=1}^{n}\left(\left.\nabla_{\gamma} F(\gamma(\alpha))\right|_{\gamma(\alpha)=(1-\alpha) x+\alpha \bar{x}, \alpha=k / n}\right)\right]_{i}[\bar{x}-x]_{i}\right| ∣ ∣ [ n 1 k = 1 ∑ n ( ∇ γ F ( γ ( α )) ∣ γ ( α ) = ( 1 − α ) x + α x ˉ , α = k / n ) ] i [ x ˉ − x ] i ∣ ∣ 实验效果 在分类问题中的效果
在自然语言中的效果
integrated_gradients
Saliency Maps Picture